Toni Westbrook dot Com

The Joy of Computer Science and Engineering

Continuing on posting some past work to get the blog up to date, here are some graphs showing completion of the Hodgkin Huxley method of processing voltage gated ion channels. At this point, the neural network supports adding ion channels to the plasma membrane with different gating types, including voltage gates as well as voltage gates with inactivation gates (as well as ion pumps, though these are not processed by HH).

Akin to how protein subunit types give rise of the type of channel and gates of a physical ion channel, attributes associated with a SynthNet ion channel control what kind of channel and gates it possesses. Additional properties such as membrane threshold potential, permeability, and refractory period control the behavior of the voltage gated ion channels.

Below are some graphs with a two connected neural processes, the latter containing voltage gated sodium channels (with inactivation gates) and voltage gated potassium channels, constructed to behave as normal neural structures do during the action potential process. The first structure (membrane potential shown in blue) was clamped at -30mV for different periods of time in each graph. Shown is red is the membrane potential of the second structure. The left graphs show regular firing with different refractory periods, while the right graphs show burst and oscillating potentials (caused by the rate and magnitude of repolarization remaining higher than the threshold potential, coupled with a very short refractory period).

In the next post, I’ll be showing the interaction of action potential (via HH) and electrotonic potential (via cable and capacitance calculations) over a more complex morphology.

Though I haven’t updated the blog in a while, I’ve really been going full-steam on the neural emulator. I’ve been taking screenshots as I go, so over the next day or so I’m going to try to make a few posts with those shots to get everything up to speed on the blog. Also, thanks for all the comments on other posts! I’ll be getting back to them soon (this weekend).

The first big update concerns processing electrotonic potential across the cell and the plasma membrane. In my previous post, I talked a bit about using the cable equation for distribution of current. As of now, I still make use of the cable equation for distributing potential across the cell. This takes into account the length and circumference of the segment in question, in addition to internal resistance, and resistance across the plasma membrane. Also, in order to appropriately address membrane moieties, calculations will also take into account the capacitance of the membrane. This allows not only a more realistic build-up of potential to occur to allow things like temporal summation to work properly, but also allow us to emulate myelination, in which electrotonic potential is subjected to a change in attenuation due to higher resistance and lower capacitance of the plasma membrane.

Below is a membrane potential graph generated from a simple structure consisting of 3 segments. The first segment is clamped with oscillating voltage, with structure 2 connected to 1, and 3 to 2. We can see the subsequent structures increase and decrease according to their distance from structure 1. The curve is controlled by the capacitance and resistance of the plasma membrane:

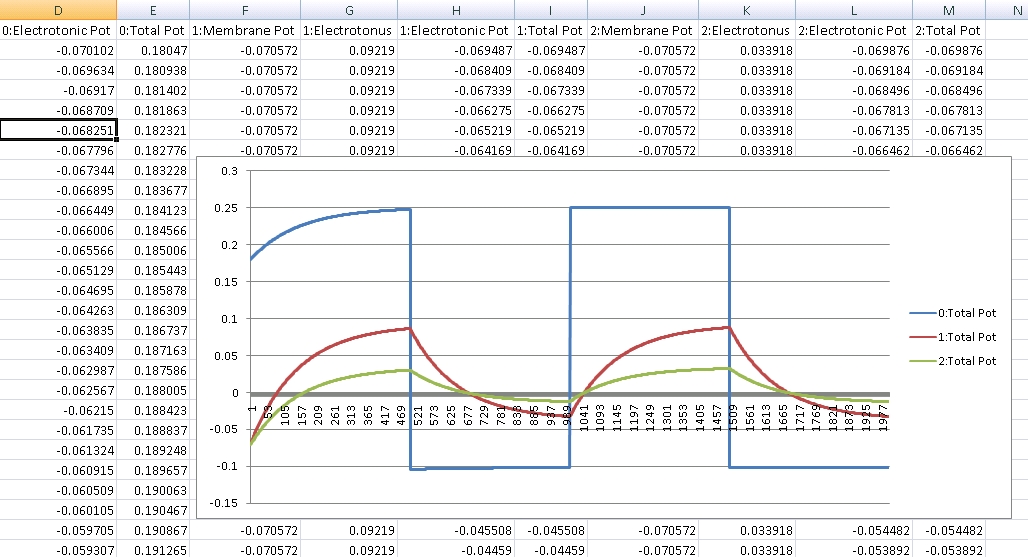
Note that membrane resistance is calculated via ionic permeability. This is a simple graph and the following posts will show some more interesting graphs with the effects of spatial summation and changes in resistance illustrated, but this one is very clear at showing the expected curve associated with a capacitor.

Next post illustrates the completion of Hodgekin-Huxley calculations for voltage-gated ion channels.